hcnak.blog

posted at 2015-12-09 01:07:45 +0000

高精度计算详解（加法）与其C++实现

这个源于一道ACM题，显示在杭电OJ上面看到了计算2个15位数字的和，咋一看，以为很简单，结果被坑惨了。后面在自己学校的题里面看到了输出斐波拉契数列的前1000项，我查了查第1000项，卧槽，真的好长。

斐波拉契数列第1000项：43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875

要想计算输出这些的话，用那些编程语言自带的数据类型肯定不行，所以这里就自然想到了分别处理这个数字的每一位，当然，还有更优的方法是，分别处理数列的每几位。我们这里就讨论把数字的每一位提取出来进行处理吧。

来自百度百科：对于非常庞大的数字无法在计算机中正常存储，于是，将这个数字拆开，拆成一位一位的，或者是四位四位的存储到一个数组中，用一个数组去表示一个数字，这样这个数字就被称为是高精度数。

当然，这里给出维基百科，高精度计算页面

因为我这里只是简单的讨论高精度计算，所以这里只讨论最简单的，即高精度加法，至于乘法和除法，我会在以后补上。

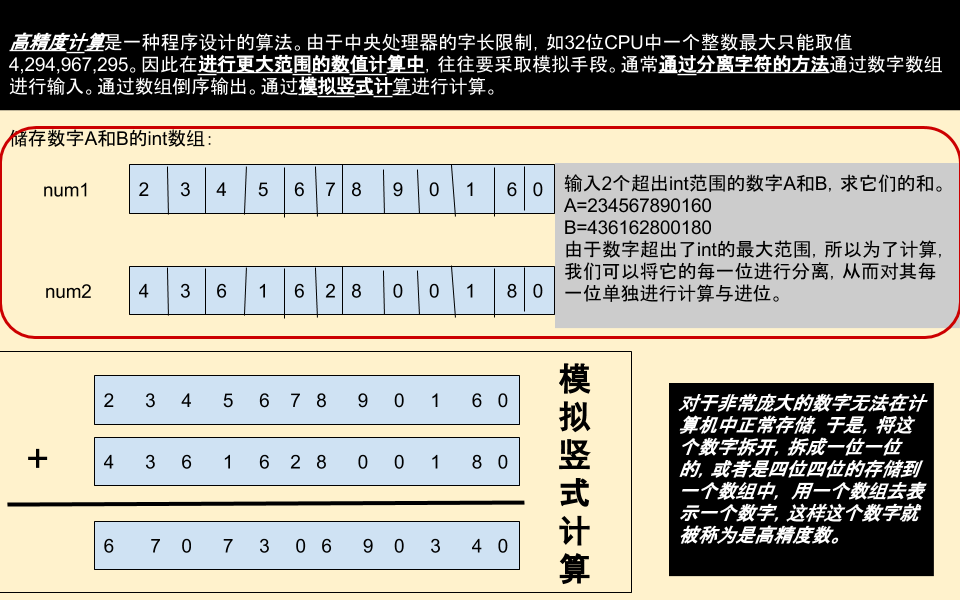
先来从一张图看看高精度计算中的加法：

所以，要实现高精度计算，我指的是加法，我们只需要实现以下2点：

把一个数字的每一位单独储存
对数字的每一位相加，手工进位

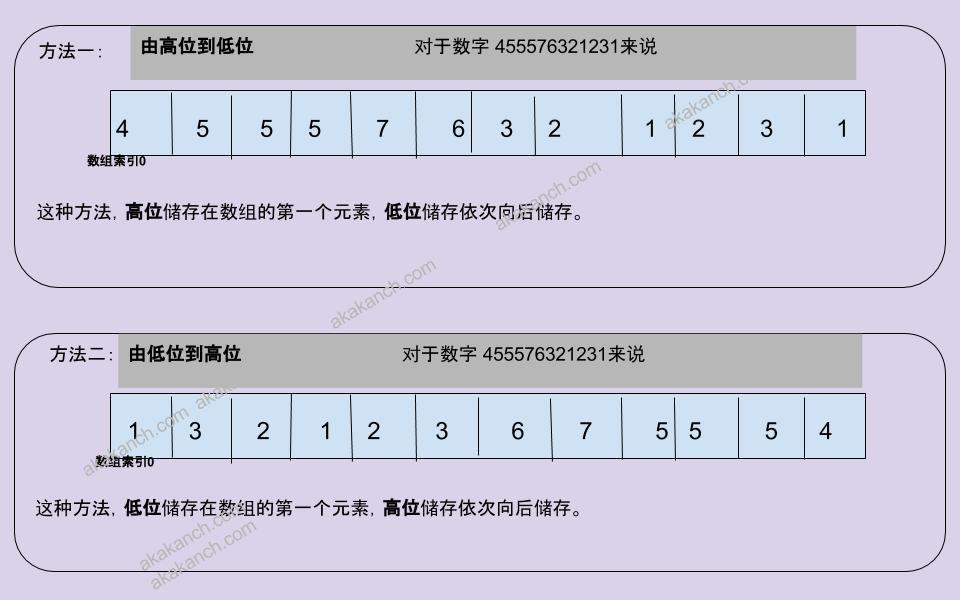
再来讲讲如何单独储存数字的每一位。有2种方法，第一种当然是按照正常的顺序，

大家可以从上图清晰的看到，采用第二种方法储存数位，最便于我们编写代码进行表达与相加。

所以，若采用第二种方法，我们就可以把每次每个数位的相加表达成以下方法：

rebuf[i] = nabuf[i] + nbbuf[i] + X;
X = rebuf[i] / 10;
rebuf[i] = rebuf[i] % 10;

另外，因为我们采取了方法二来储存，缺点就是，我们在传入2个数字后要对其进行反转，然后计算完毕后，再反转回来。

这里就有一个小问题：如果数字A或者B是100000这种，反转后就变成000001，相加后结果可能会出现 000000100这种情况，再将结果反转就变成了001000000。

所以，我们还需要一段代码处理这个结果，把前面的0都去掉，当然，如果存在的话。毕竟我们需要的只是相加后的结果。

 X = 1;
 for (int i = loop; i >= 0; i--) {
   if (rebuf[i] == 0 && X == 1) {
     continue;
   }
   X = 0;
   result += (rebuf[i] + '0');
 }

最终它的代码，我是指这个大数相加的函数代码如下：

string AddNum(string & na, string & nb) {
  int rebuf[1001] = {
    0
  }, nabuf[1001] = {
    0
  }, nbbuf[1001] = {
    0
  };
  int X = 0, nalen = na.length(), nblen = nb.length(), loop = nalen;
  if (nalen < nblen) {
    loop = nblen;

  }
  for (int i = nalen - 1; i >= 0; i--) {
    nabuf[nalen - 1 - i] = na[i] - '0';
  }
  for (int i = nblen - 1; i >= 0; i--) {
    nbbuf[nblen - 1 - i] = nb[i] - '0';
  }
  //start cal
  for (int i = 0; i < loop; i++) {
    rebuf[i] = nabuf[i] + nbbuf[i] + X;
    X = rebuf[i] / 10;
    rebuf[i] = rebuf[i] % 10;
  }
  rebuf[loop] += X;
  //to string
  string result = "";
  X = 1;
  for (int i = loop; i >= 0; i--) {
    if (rebuf[i] == 0 & amp; & amp; X == 1) {
      continue;
    }
    X = 0;
    result += (rebuf[i] + '0');
  }
  return result;
}

这里我们只讨论了加法，减法和加法类似。

乘法和除法我大概会在以后补出来。

last updated on 2022-07-27 01:57:54 +0000